INTERPRETING THE NUMBERS
| ATOMIC MASS and
ISOTOPES: INTERPRETING THE NUMBERS |
 |
| Particle | Mass (amu) |
Mass
(g x1024) |
Charge |
Charge (Coulombs x1019) |
Diameter (meters x1015) |
protons | neutrons | electrons | % abundance | half life (yr) |
| Proton | 1.007277 | 1.6726 | 1 | 1.602 | 1.7 | 1 | 1032 | |||
| Neutron | 1.008866 | 1.6749 | 0 | 0 | 1.6 | 1 | 1.94x10-5 | |||
| Electron | 0.000549 | 0.000911 | -1 | -1.602 | ~0.001 | 1 | > 6.6×1028 | |||
|
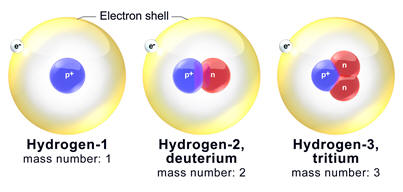
Hydrogen-1 |
1.007825 | 1.6736 | 0 | 0 | 5.0x104 | 1 | 0 | 1 | 99.9885 | |
| Hydrogen-2 | 2.014102 | 3.3445 | 0 | 0 | 1 | 1 | 1 | 0.0115 | ||
| Hydrogen-3 | 3.016049 | 5.0082 | 0 | 0 | 1 | 2 | 1 | 12.5 | ||
| Cabon-12 | 12.00000 | 19.926 | 0 | 0 | 1.4x105 | 6 | 6 | 6 | 98.93 | |
| Carbon-13 | 13.003355 | 21.593 | 0 | 0 | 6 | 7 | 6 | 1.07 | ||
| Carbon-14 | 14.003241 | 23.253 | 0 | 0 | 6 | 8 | 6 | 5730 | ||
| Uranium-234 | 234.041 | 3886.3 | 0 | 0 | 3.50x105 | 92 | 142 | 92 | 0.0055 | 2.455x105 |
| Uranium-235 | 235.044 | 3903.3 | 0 | 0 | 92 | 143 | 92 | 0.72 | 7.04x108 | |
| Uranium-238 | 238.051 | 3952.9 | 0 | 0 | 92 | 146 | 92 | 99.2745 | 4.5x109 |
Giant leaps by humankind have positively impacted the progress of many scientific fields. Evolution and the genetic code in RNA and DNA, Newton's Laws of Motion and Einstein's Relativity Theories, Plate Tectonics, Galileo's improved telescope and the Periodic Table forever advanced their respective branches of science. The periodic table developed in 1869 by Dmitri Mendeleev was the culmination of the contributions of the work of many chemists. Today's table has many additions and improvements but bears a substantial resemblance to the original Mendeleev table. Amazingly, the Mendeleev table preceded the discovery of protons, neutrons and electrons and was based on experimental observations of the relative atomic masses of the elements and physical and chemical properties of the elements. Today, theoretical studies have produced results consistent with the arrangement of the periodic table. The element boxes in most periodic tables contain at least the symbol for the element, the atomic number and mass of the element. This discussion focuses on atomic mass values and the relationship of the values to isotopes.
Mendeleev did not have information about atomic composition and arranged the elements according to increasing atomic mass. This arrangement worked for most but not all elements. As an example, Mendeleev switched the positions of tellurium and iodine because he decided that the atomic mass values were probably in error. The switch was needed to align the elements in groups based on their properties. The switch was a wise move but based on the incorrect assumption that the atomic mass measurements contained errors. Iodine does have an atomic mass lower than the atomic mass of tellurium. But as Henry Moseley demonstrated in 1913, the periodic table needs to be arranged according to increasing atomic number (# of protons in the nucleus) rather than atomic mass (See http://murov.info/timelines.htm for timeline of developments in chemistry). Atomic mass generally correlates well with atomic number but there are exceptions. The discovery of protons in 1886 and electrons in 1897 helped lay the foundation for Moseley's ground breaking discovery that the atomic number is the appropriate variable for arranging the elements in ascending order. The existence of neutrons was suspected as early as 1886 by Crooke to account for non-unity atomic mass values but it was not until 1932 that Chadwick provided sound evidence for the existence and properties of neutrons.
1Q. In addition to tellurium and iodine, name the other
pair(s) of elements that would be placed incorrectly in a periodic table
arranged by atomic mass. ANSWER to question 1.
To jump to answer to question 1, please click on
ANSWER to question 1.
In addition to arranging the elements is ascending order by atomic mass, Mendeleev started new periods to align the elements with similar properties in columns or groups. For instance, Li, Na, K, Rb and Cs all have similar chemical reactivity (all react very quickly with water to form a hydroxide and hydrogen gas) and form compounds with the same ratio of cations to anions (e.g., LiCl, NaCl, KCl, RbCl, CsCl and Li2O, Na2O, K2O, Rb2O and Cs2O). We know today that each element has one more proton and electron that the preceding one. In the table above, in amu units, protons and neutrons weigh 1.0 amu to two significant figures and 1.01 amu to three significant figures. The mass of electrons do not contribute to the mass to the tenth position. It should be noted that the masses of protons, neutrons and electrons are not exactly additive when they are put together to form atoms. A small but significant binding energy affects the sum in the second digit after the decimal. While an awareness of the binding energy is important, most of this discussion will only consider the first digit after the decimal and the binding energy needs to be considered only for a more technical discussion of atomic mass.
The simplest element (hydrogen) includes only a proton and electron (charge must be balanced for a neutral atom). This would give hydrogen an atomic mass of 1.0 amu/atom. The next element would be expected to have two protons and two electrons. But a problem is encountered because the experimental atomic mass of helium is 4.0 amu/atom. Chadwick's discovery of the neutron provides an explanation for a mass that is double the expectation. The most common helium nucleus contains two neutrons in addition to the two protons. Since protons and neutrons have a mass of 1.0 amu/particle, the atomic mass is the sum of the number of protons and neutrons or the number of neutrons is equal to the atomic mass minus the atomic number. It should be emphasized that the result of the mass minus the atomic number gives not the number of neutrons but the average number of neutrons.
2Q. Give the number of protons, neutrons and
electrons in F, Na, P, As, I, Tb, Au.
ANSWER to question 2.
3Q.
Which statement is true about the number of neutrons compared to the number of
protons for the elements? a. the numbers are about equal
b. the number of neutrons seems to be random.
c. the
number of neutrons is close to the same as the number of protons for the first
20 elements and then increases by an average of more than one after the first 20
elements. d. none of the preceding answers.
ANSWER to question 3.
Technically, protons and neutrons (both are hadrons) are not basic particles. Each is made up of three quarks. However, quarks do not need to be considered to explain chemistry concepts and the development of the periodic table. In the simplified concepts presented here, protons, neutrons and electrons will be considered to be the building blocks of the elements.
We now skip ahead to chlorine with atomic
number 17 and atomic mass 35.453. Based on these numbers, chlorine should
have 17 protons and electrons and 18.5 neutrons. Since fractional numbers
of basic particles are not possible, another explanation is needed. The
values of atomic mass are determined by quantitative chemical experiments or
alternatively by mass spectrometry. Quantitative chemical experiments
yield the average atomic mass. The value of 35.453 can most easily be
explained by the presence of two different types of chlorine atoms with
different numbers of neutrons. These atoms with the same number of protons
and electrons but different numbers of neutrons are called isotopes. By
looking at the numerous fractional atomic mass values in the periodic table, it
is easily observed that many elements must have two or more naturally occurring
isotopes. The information provided by the atomic mass will be discussed
later but only very limited information on the number and abundance of each
isotope is discernable from the atomic mass. Crooke in 1886 and Soddy in 1913 suggested that isotopes needed
to exist to explain several atomic mass values. In 1922, Francis Aston was
able to demonstrate the existence of isotopes using a mass spectrometer.
Chadwick in 1932 with the discovery of the neutron was able to explain the
composition of isotopes. As mentioned earlier in this paragraph, in
addition to chemical measurements, mass spectrometry can be used to determine
average atomic mass. Mass spectrometry also shows which isotopes exist and
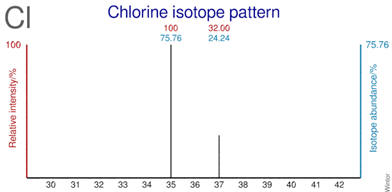
their relative abundance. As an example, the simulated mass spectrum of chlorine
atoms is shown to the right. Mass spectrometry separates atoms (actually cations) by mass and gives signal
intensity related to the amounts of each isotope.
We now need to examine several issues:
1. What information about isotopes can be extracted from the atomic mass.
2. Do the physical and chemical properties vary from one isotope to
another.
2. Is there a way to predict which isotopes should exist.
3. How do the number of neutrons affect the nuclear stability of an
isotope.
4. Do different isotopes have different applications.
ISOTOPE COMPOSITION. Mass spectrometers are expensive and often not available
for determination of atomic mass values. Quantitative chemical experiments
provide average atomic mass values but do provide limited information on the
number and abundance of isotopes. First, if the atomic mass is within 0.08
of a whole number, it is likely that there is predominance of one isotope.
Otherwise, the mass values for the isotopes would have to coincidentally average
out to close to a whole number. There are some rare instances of this but
for the most part, an atomic mass close to a whole number enables the conclusion
that there is probably one main isotope. Basing your answer only on the
periodic table, answer the following exercises:
1. How many neutrons are in aluminum? 26.982 - 13 = 13.982.
The definite conclusion is that aluminum has an average of 13.982 neutrons and
probably a predominance of one isotope with 14 neutrons. Without
additional information, the word average needs to be included as the value could
be the result of two or more isotopes coincidentally averaging out close to a
whole number. In reality, aluminum has only one naturally occurring
isotope but this cannot be ascertained from the periodic table.
2. How many neutrons are in magnesium? 24.305 - 12 = 12.305.
There is an average of 12.3 neutrons and more than one isotope of magnesium must
occur naturally. Otherwise the atomic mass would be much closer to a whole
number. With only medium confidence, it is ok to suggest that one of the
isotopes and probably the major one has 12 neutrons but additional speculation
is not warranted. Isotope tables reveal that there are three naturally
occurring magnesium isotopes: magnesium-24 - 78.99%, magnesium 25 -
10.00%, magnesium 26 - 11.01%.
4Q. State your conclusions about the number of neutrons in Sc, Cu, Pb. ANSWER to question 4.
 ISOTOPE
BEHAVIOR.
Do isotopes play a significant role in chemistry? Chemical reactions
involve electronic changes that have very limited dependence on atomic mass. Early in the periodic table, isotope behavior can differ
because there can be a significant percent difference in atomic mass values.
For instance lithium-6 has a mass of about 15% less than the mass of lithium.
There can be small mass effects on the rates of chemical reactions and also
effects on physical properties such as density. At high atomic mass
values, the percent difference in mass between isotopes tends to be smaller with
only very small observable effects on reaction rates and physical properties.
It should be noted that even small differences can be useful and are actually used to
separate uranium-235 from uranium-238. This separation will be discussed
later. For almost any generalization that can be stated about elements, it
is very common to have to add "except for hydrogen." Hydrogen-1 and
hydrogen-2 (see first table) differ in mass not by a small percent by by a
factor of 2. The density of D2O is about 11% higher than the
density of H2O. The melting point of D2O is 3.8oC.
Reaction rates that directly involve the breaking of the carbon-hydrogen bond
are often about seven times slower for deuterium (hydrogen-2) compared to hydrogen-1.
ISOTOPE
BEHAVIOR.
Do isotopes play a significant role in chemistry? Chemical reactions
involve electronic changes that have very limited dependence on atomic mass. Early in the periodic table, isotope behavior can differ
because there can be a significant percent difference in atomic mass values.
For instance lithium-6 has a mass of about 15% less than the mass of lithium.
There can be small mass effects on the rates of chemical reactions and also
effects on physical properties such as density. At high atomic mass
values, the percent difference in mass between isotopes tends to be smaller with
only very small observable effects on reaction rates and physical properties.
It should be noted that even small differences can be useful and are actually used to
separate uranium-235 from uranium-238. This separation will be discussed
later. For almost any generalization that can be stated about elements, it
is very common to have to add "except for hydrogen." Hydrogen-1 and
hydrogen-2 (see first table) differ in mass not by a small percent by by a
factor of 2. The density of D2O is about 11% higher than the
density of H2O. The melting point of D2O is 3.8oC.
Reaction rates that directly involve the breaking of the carbon-hydrogen bond
are often about seven times slower for deuterium (hydrogen-2) compared to hydrogen-1.
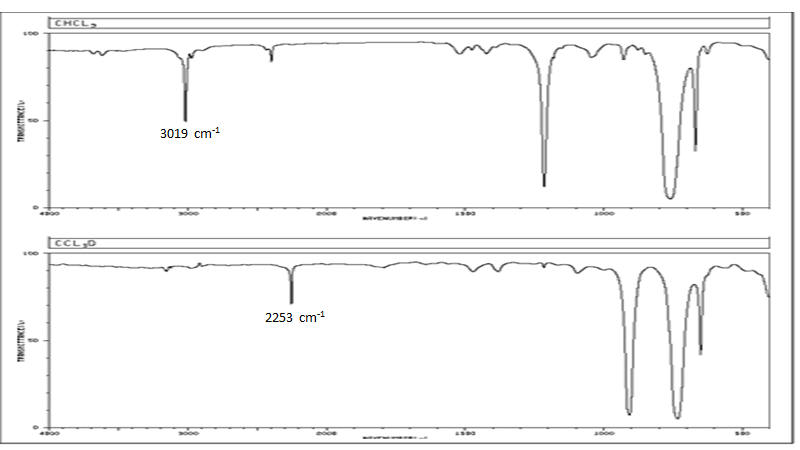
Another example of a significant difference between H-1 and H-2 can be illustrated with the use of infrared spectra. IR spectra contain energy absorptions that activate vibrational modes in the molecule. For some vibrations, a model with 2 balls on the ends of a spring often suffices. The IR spectra to the right are for the molecules of
chloroform (CHCl3) and chloroform-D (CDCl3). Notice that there are significant differences in the spectra with the replacement of the H by a D. For the focus of this discussion, the C-H bond stretch is at an energy of 3019 cm-1 and the C-D stretch is at 2253 cm-1. The ratio is close to the ratio predicted by the equation for 2 balls on a spring (Hooke's Law). This discussion has been included just to illustrate that for hydrogen, there are behavior differences for isotopes because of the factor of 2 difference in atomic mass values.
As contrasted with chemical and physical properties, nuclear properties and stability do depend on the ratio of protons to neutrons (the nuclear stability of isotopes can be very different).
 ISOTOPE
STABILITY. Determination of the stability of an isotope is beyond the
scope of this treatment. However, based on empirical observations, it is
possible to come up with some useful generalizations. First, in most cases,
if an isotope has a number of neutrons very close to the number of neutrons
calculated by subtracting the atomic number from the atomic mass, the isotope is
probably a stable isotope of the element.
If, on the other hand, the number of
neutrons differs significantly from the difference between the atomic number and
atomic mass, there is a significant chance the nucleus is unstable. For
example, if the question is about the stability of oxygen-16, the response would
be that this isotope would likely be stable as the difference between the atomic
number and atomic mass for oxygen is 7.999. In reality, there are three
stable isotopes of oxygen but oxygen-16 composes 99.757% of naturally occurring
oxygen isotopes. For oxygen-19, the difference of three between the number
of neutrons and the average calculated from the periodic table leads to a
suspicion that the isotope could be unstable. In reality, oxygen-19 has a
half life of about 26 seconds.
ISOTOPE
STABILITY. Determination of the stability of an isotope is beyond the
scope of this treatment. However, based on empirical observations, it is
possible to come up with some useful generalizations. First, in most cases,
if an isotope has a number of neutrons very close to the number of neutrons
calculated by subtracting the atomic number from the atomic mass, the isotope is
probably a stable isotope of the element.
If, on the other hand, the number of
neutrons differs significantly from the difference between the atomic number and
atomic mass, there is a significant chance the nucleus is unstable. For
example, if the question is about the stability of oxygen-16, the response would
be that this isotope would likely be stable as the difference between the atomic
number and atomic mass for oxygen is 7.999. In reality, there are three
stable isotopes of oxygen but oxygen-16 composes 99.757% of naturally occurring
oxygen isotopes. For oxygen-19, the difference of three between the number
of neutrons and the average calculated from the periodic table leads to a
suspicion that the isotope could be unstable. In reality, oxygen-19 has a
half life of about 26 seconds.
5Q. Comment on the likely stability of cobalt-59 and nitrogen-17. ANSWER to question 5.
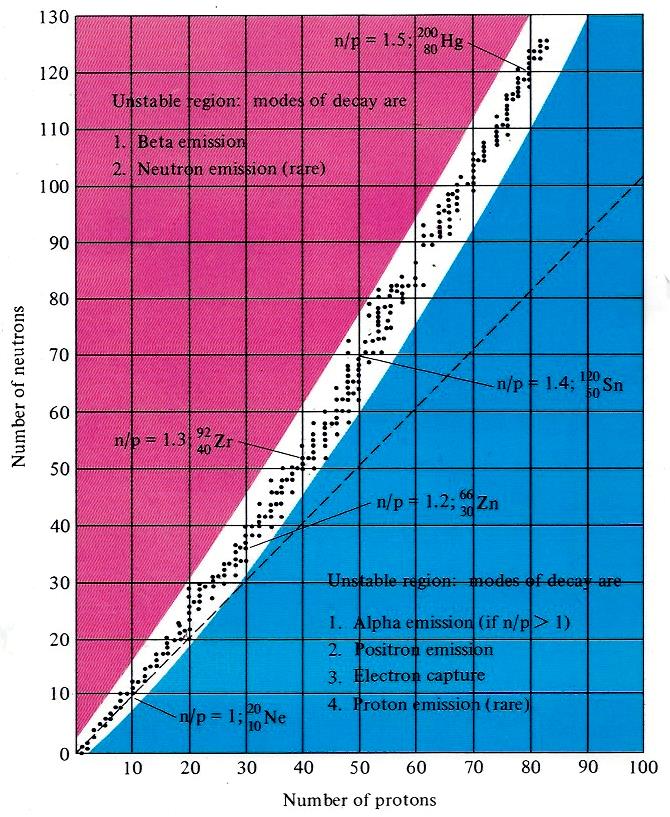
The chart to the right is a graph of the number of neutrons vs the number of protons. The black dots show that the stable isotopes fall in the rather narrow white region. The combinations that fall in the blue or magenta are unstable and if made, decay radioactively. Up through calcium (atomic number 20), the number of protons and neutrons are within one of equality except for argon. After calcium, on average, more than one neutron is added with the addition of each proton. For uranium, there are about 1.6 times as many neutrons as protons. Possibly this provides more separation of the positively charged protons. By inspecting the number of dots as a function of atomic number, there are many elements with only one naturally occurring isotope but most have more than one with a couple of elements even having nine stable isotopes.
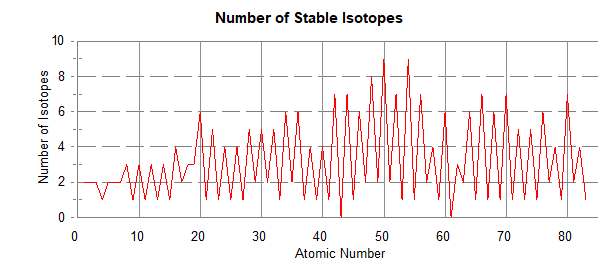
A graph of the number of isotopes as a function of atomic number in the figure above reveals a saw tooth graph. There are clearly more isotopes for even numbered elements than odd and usually only one or two for the odd numbered elements. Odd atomic numbered technetium and promethium do not have any stable isotopes and all elements after lead have some degree of radioactivity (for half lives of radioactive isotopes, see: https://en.wikipedia.org/wiki/List_of_radioactive_nuclides_by_half-life. The empirical conclusion is that the most stable combinations of protons and neutrons in descending order of stability are even-even, even-odd, odd-even and odd-odd. There are only a few cases of stable nuclei with odd numbers of protons and neutrons with only one of the odd-odd being the most abundant isotope. Nitrogen-14 is an odd-odd and makes up 99.632% of naturally occurring nitrogen on earth. Using these guidelines, comment on the number of neutrons in bromine. Bromine has an atomic number of 35 and an atomic mass of 79.904. Without thinking deeper, it will be tempting to conclude that bromine has predominantly one naturally occurring isotope with 45 neutrons. However, this would be an odd-odd situation and we have noted that odd-odd combinations are rare and not abundant. Checking the abundance of bromine isotopes reveals that bromine has two naturally occurring isotopes: bromine-79 and bromine-81 with abundances of 50.69% and 49.31%. Thus the average atomic mass is about 80 and demonstrates that looking at the atomic mass alone is not sufficient.
6Q. Based on the periodic chart, now many
neutrons are present in: Ar, Co, Ni, Ag, I.
ANSWER to question 6.
UNSTABLE ISOTOPES. There is a
high probability that combinations of protons and neutrons not represented by a
black dot in the figure above are unstable and radioactive. Other proton
to neutron ratios have not yet been discovered and are likely unstable. Unstable
combinations undergo nuclear changes that result in new proton to neutron
ratios. However, the grass is not always greener on the other side of the
fence and the change often results in a new unstable nucleus.
a and
b decay are two of
the most common radioactive decay reactions that change the proton to neutron
ratio. An alpha particle is a helium nucleus or a particle containing two
protons and two neutrons. This lowers the atomic number by two and the
atomic mass by four units. A beta particle is an
electron and results from the decomposition of a neutron into a proton and
electron. This results in an increase of one in atomic number and
effectively no change in the atomic mass. Most decays also include the emission
of gamma rays and some only gamma rays.

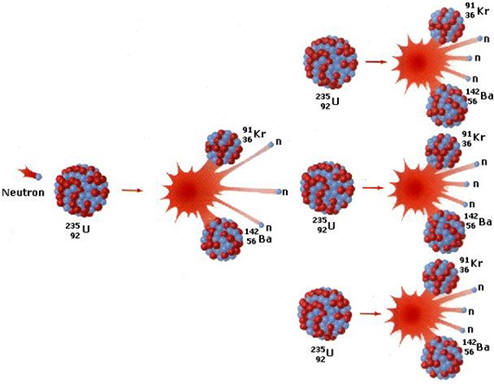
| Notice that there are predominantly two isotopes of uranium. The periodic table includes an atomic mass of 238.03 g/mole (or amu/atom) for uranium. This strongly indicates that most uranium on earth is U-238. Experimentally, naturally occurring uranium is composed of 99.3% U-238 and 0.7% U-235. In the late 1930's, it was discovered that when U-235 is impacted by a neutron, the uranium nucleus cleaves by one of at least two pathways and yields the nuclei of two smaller elements along with 2 or 3 neutrons. If these neutrons go on to impact more fissionable nuclei, more neutrons will be released. One neutron can initiate the reaction but the release of more than one neutron by the reaction means that the reaction can continue in an escalating way or a chain reaction that leads to a nuclear explosion. To sustain the chain reaction, a critical mass must be present or neutrons will go un-captured and the reaction will not be sustained. If the numbers of neutrons released is controlled, it is possible to use this reaction as a source of energy that can be converted into electricity. The products weigh slightly less than the reactants resulting in the release of substantial energy. Unlike chemical reactions where the mass change is too small to measure, the mass lost here is much greater and the amount of energy released is much more than for a chemical reaction. |
 |
|
Because U-238 does not undergo fission, to build a nuclear reactor or a
bomb, it is necessary to start with uranium ore that contains only 0.7%
U-235 and enrich the U-235 to a sufficient percentage that a nuclear
reaction can be sustained. Because the two uranium isotopes have very
similar physical and chemical properties, separating the isotopes is a
technologically difficult, expensive and time consuming process. Put
very simply, one of the techniques involves making the uranium into UF6 and
taking advantage of the property that it can be converted into a gas at
a reasonably low temperature. The slightly lighter gas molecules of UF6 with
U-235 move a little faster than those of U-238. By repeating a
procedure that takes advantage of this velocity difference many times,
it is possible to enrich the uranium in U-235 enough for a nuclear
reactor and more for a bomb. The controversial Iran nuclear treaty
involves the issues discussed above. Iran would like to enrich uranium
and they have the centrifuges needed to do this. Iran claims that they
want to enrich the uranium enough to use in peaceful nuclear energy
facilities. Bomb enrichment requires even higher percentages of U-235
than energy facilities require. The treaty restricts Iran to preparing
the U-235 sufficient for energy facilities but insufficient for bomb
use. Some people and countries do not believe that Iran will abide by
the rules. Unfortunately, nuclear fission is fraught with many problems. Radioactive waste is created that is dangerous for thousands of years and disposal and storage methods have not been satisfactorily addressed. There have been three major nuclear accidents at nuclear plants although new designs should reduce the risk. While it might appear that fuel is available, the enrichment of U-235 or the production of Pu-239 both have significant cost. There is also the real problem that weapons grade fissionable material could get into the wrong hands and result in a disastrous situation. |
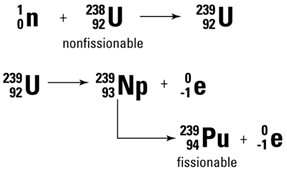
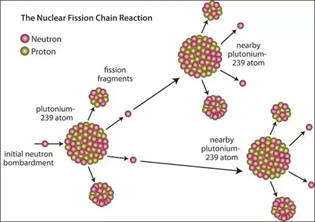
| Although U-238 does not fission when impacted by neutrons, neutrons are captured which convert the U-238 into Pu-239. Pu-239 does undergo fission and can also be used to make bombs. At the end of WWII, two bombs were dropped in Japan. One was a U-235 bomb and the other was a plutonium bomb. Other isotopes of heavy elements also undergo fission. |
 |
 |
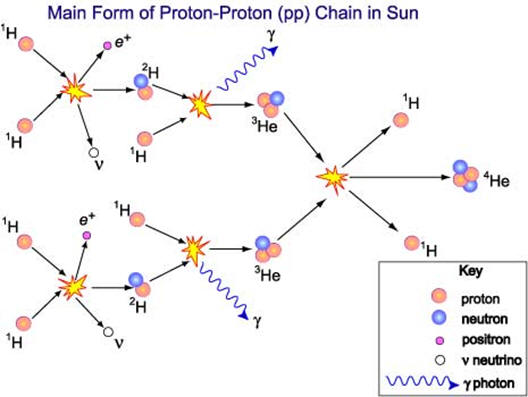
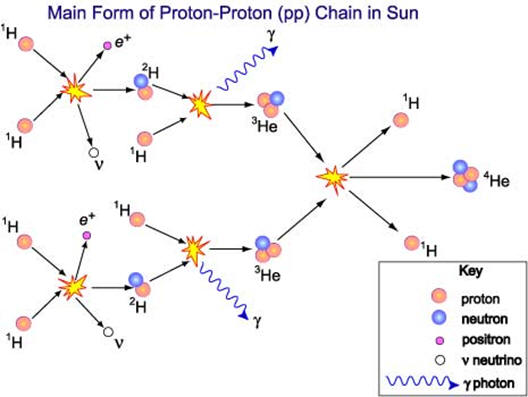
| It was mentioned above that the fission process is accompanied by a mass loss that results in a huge energy release. The graph to the right shows the stability of nuclei as a function of atomic mass. Iron-56 is the most stable nucleus. When uranium undergoes fission, two lighter and more stable nuclei are produced along with the release of energy. Notice that there is a much greater move toward stability when hydrogen atoms are fused and produce nuclei such as helium that are more stable than hydrogen. This is the process illustrated below that occurs in the sun. The process below shows the production of He-4. Stars are composed primarily of hydrogen and can sustain hydrogen fusion reactions until the hydrogen drops too low. 91% of the atoms in the universe are hydrogen atoms and most of the rest is helium. Additional fusion reactions in stars produce elements up through iron. Several countries have been able to design and construct bombs based on nuclear fusion reactions although not using hydrogen-1 fusion. Considerable research continues to find ways to harness nuclear fusion. If and when successful, nuclear fusion could be an answer to our energy and climate change issues. Fusion has minimal nuclear waste issues, cannot undergo a meltdown type of event and fuel is cheap and abundant. | 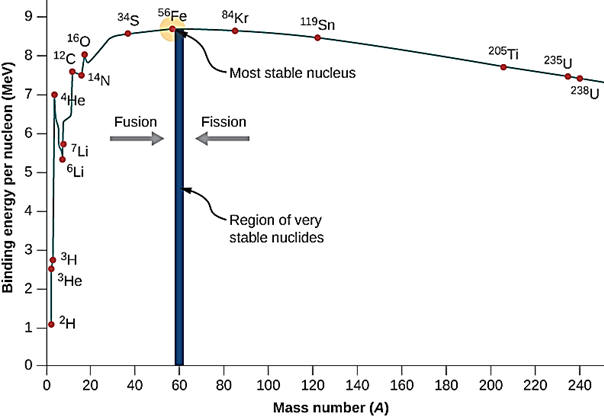 |
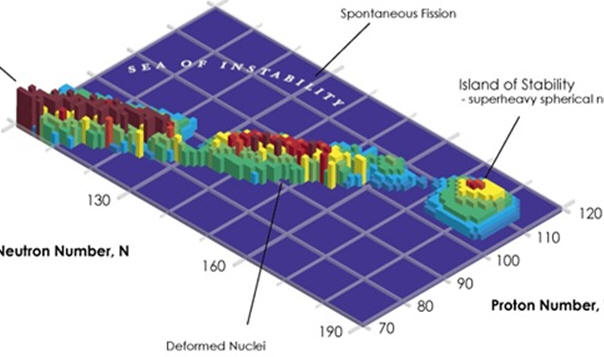
 TRANSURANIUM ISOTOPES. It was mentioned that no nucleus with more than 82 protons has yet to be found that is stable. Because of half lives on the order of or longer than the life of our solar system (4.5 billion years), elements with up to 92 protons have been found to occur naturally on earth. Except for trace amounts of plutonium, all elements with more than 92 protons must be prepared in the laboratory using nuclear methodology. Generally, the more the number of protons, the shorter the half life as illustrated in the graph below. However, it should be noted that synthetic methods do not necessarily make the most stable isotopes. It is possible that some longer lived isotopes will be synthesized in the future. One particular point of interest are elements with magic numbers and those with an atomic number of 114. Some calculations predict that some isotopes with 114 protons should be on an island of stability and have longer half lives than other isotopes near them. https://en.wikipedia.org/wiki/Island_of_stability#:~:text=In%20nuclear%20physics%2C%20the%20island,and%20long%2Dlived%20primordial%20radionuclides. https://en.wikipedia.org/wiki/Magic_number_(physics) |
ISOTOPE APPLICATIONS.
In chemistry, isotopes are a very
valuable tool for the exploration of mechanisms of reactions. Use of an
isotope in a critical part of a molecule enables the researcher to follow
changes that the atom undergoes. Also isotopes change the rates of
reactions in predictable ways and provide insight into the steps during the
course of a reaction. From a nuclear standpoint, isotopes differ widely in
their behavior. A prime example was discussed above using uranium as an
example. For more information, please visit:
https://en.wikipedia.org/wiki/Isotope
,
https://chem.libretexts.org/Courses/Eastern_Mennonite_University/EMU%3A_Chemistry_for_the_Life_Sciences_(Cessna)/11%3A_Nuclear_Chemistry/11.4%3A_Uses_of_Radioactive_Isotopes
https://courses.lumenlearning.com/boundless-chemistry/chapter/use-of-isotopes/
https://www.hutton.ac.uk/research/departments/environmental-and-biochemical-sciences/isotope-applications
,
https://www.britannica.com/science/radioactive-isotope
,
https://www.frontiersin.org/articles/10.3389/fevo.2016.00020/full ,
|
ANSWERS 1A. Co, Ni Th, Pa U, Np Pu, Am Return to question 1. 2A.
3A. c. Return to question 3. 4A. a. Scandium has an average of 24 neutrons. Since the average is within 0.08 of a whole number, there is high probability that there is a predominance of only one isotope of scandium. Actually only scandium-45 has been found to occur naturally on earth. b. Copper has an average of 31.546 neutrons. The value is not close to unity leading to the definite conclusion that copper has more than one naturally occurring isotope with significant abundances of at least two isotopes. Isotope tables reveal that copper has two naturally occuring isotopes: 69.17% copper 63 and 30.83% copper 65. Notice that both stable isotopes have an even number of neutrons. c. Lead has an average of 125.2 neutrons. The value is more than 0.08 from unity leading to the conclusion that there are at least two naturally occurring isotopes of lead. With a lower confidence, there could be a predominance of lead-207. Isotope tables reveal that lead has four naturally occurring isotopes but the previous conclusion about lead-207 was not accurate as the actual abundances are: 1.4% lead-204, 24.1% lead-206, 22.1% lead-207, 52.4% lead-208. Lead has an even number of protons so having four stable isotopes is not unexpected. Also note that 3 of the 4 stable isotopes also have even numbers of isotopes. Return to question 4. 5A. a. Cobalt has an atomic mass of 58.933. This provides evidence that cobalt-59 is the predominant of cobalt and stable. b. Nitrogen has an atomic mass of 14.007. This correctly indicates there is nitrogen-14 is the predominant isotope of nitrogen. Since nitrogen-17 differs by three neutrons from the number calculated from the periodic table, there is a strong possibility that nitrogen-17 is radioactive. This is true as nitrogen-17 has a half life of 4.2 seconds. Return to question 5. 6A.
|
This site is the first of two web sites that focus on reading between the lines on chemical concepts. The second focuses on oxidation number, electronegativity, formal charge, molecular polarity, pH, climate change and learning from mistakes. Visit: http://murov.info/oxidation.htm .For more websites by Steven Murov, please visit: http://murov.info/ . For a shorter list of chemical education sites, please visit: http://murov.info/chem.htm . To send comments or suggestions, please e-mail Steven Murov at murovs@yosemite.edu .
hit counter started 10/1/20